Uživatelské nástroje
Kódování, Shannonova věta o kódování, bezpečnostní kódy
Kódování
Kódování převádí informace jednoho typu do jiné reprezentace. Například morseovka.
Neplést si s šifrováním! U kódování je známo jak se to převádí, u šifrování ne.
Shannonova věta o kódování
Shannon's source coding theorem
Má-li diskrétní kanál kapacitu C > 0, pak použitím dostatečně dlouhých kódovaných úseků lze produkce informace H′(X) < C libovolně přiblížit k C a přitom učinit pravděpodobnost chyby libovolně malou.
- Rychlost produkce informace: H′(X) = H(X) / T
- H(X) – množství informace připadající v průměru na jeden symbol
- T – průměrný čas vysílání jednoho symbolu: T = 1 / vₘ
- vₘ – modulační rychlost
Bezpečnostní kódy
Pokud se zprávy posílají po nespolehlivém médi na kterém vznikají chyby, používají se bezpečnostní kódy. Tyto kódy umožňují chybu detekovat, a ideálně i opravit. Slovo s bezpečnostním kódem musí být vždy delší než původní slovo, dochází k redundanci.
Lineární
Lineární bezpečnostní kód je takový kód, kde libovolná lineární kombinace kódových slov je také kódové slovo.
Hammingovy
Hammingův kód (7, 4) znamená že ze 4 bitů zprávy vytvoříme 7 bitů přídáním 3 paritních bitů. Tento kód umožňuje detekovat 2 chybné bity a 1 bit opravit. Paritní a datové pity jsou uspořádány: PPDPDDD.
Potřebujeme generovací matici G a paritní matici H:
$$ G = \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ H = \begin{bmatrix} 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 \end{bmatrix} $$
Všimněte si u matice G, že řádky 3, 5, 6 a 7 reprezentují datové bity a obsahují jen jednu 1. Oproti tomu řádky 1, 2 a 4 jsou bity paritní, a označují ze kterých bitů se bude parita počítat.

Výslednou zprávu získáme vynásobením matice G zprávou (1011):
$$ \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} $$
Výsledná zpráva tedy bude 0110011.
1101 a 1011. Pokud je jich sudý počet, bude výsledek 0, pokud lichý, tak 1.
Při kontrole vynásobíme matici H zprávou:
$$ \begin{bmatrix} 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} $$
Opět můžeme použít trik se stejnými jedničkami.
Pokud vyjdou samé nuly, byla zpráva přijata v pořádku.
Pokud ne, porovnáme matici se sloupci matice H a ten u kterého se shoduje je chybný bit. Stejně tak můžeme binární čislo přečíst odzhora. Například 101 = 5, a také je to 5. sloupec v matici H.
Cyklické
Cyclic code, Cyclic redundancy check, Computation of CRC
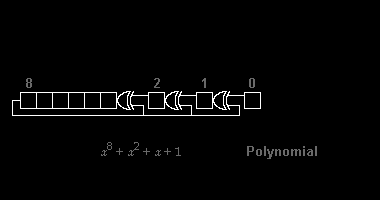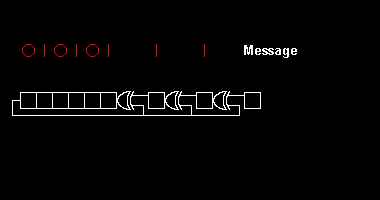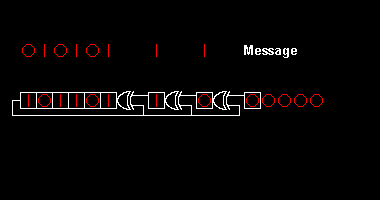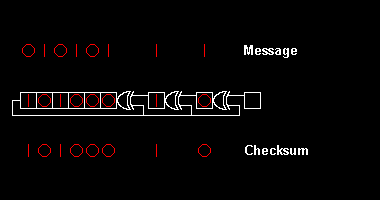 Zakódování
Zakódování 11010011101100 polynomem x³ + x + 1:
11010011101100 000 <--- ke vstupu přidáme 3 bity
1011 <--- dělitel (XOR) x³ + x + 1
01100011101100 000 <--- výsledek
1011 <--- dělitel…
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000
1011
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <---zbytek (3 bity)
Zbytek připojíme za zprávu: 11010011101100 100.
 Při kontrole postupujeme stejně, zbytek musí vyjít
Při kontrole postupujeme stejně, zbytek musí vyjít 0, jinak nastala chyba:
11010011101100 100 <--- vstup s CRC
1011 <--- dělitel
01100011101100 100 <--- vysledek
1011 <--- dělitel…
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
0 <--- zbytek
Konvoluční
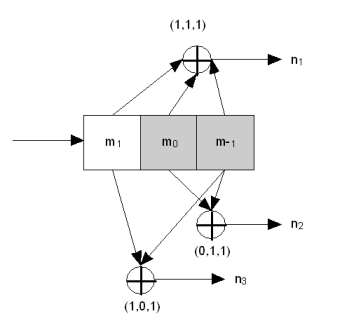
U konvolučního kódu je každý bit nahrazen n-ticí bitů. Ke kódování potřebujeme paměťové buňky a XORy. Z buněk vytvoříme posuvný registr a napojíme na ně XORy.
Na začátku obsahují všechny buňky 0. Přivedem na vstup slovo které chceme zakódovat. Jeho první bit dáme do první paměti, provedeme XORy a dostaneme n-tici. Shiftneme registr a do první buňky dáme druhý byt, XORujeme, shiftneme, … dokud nejsou v buňkých zase samé nuly.
To je také možné reprezentovat konečným automatem. Stavy jsou možné stavy pamětí, přechody podle dalšího bitu generují n-tice.
Průchod takovým automatem je mopžné vyjádřit Trellis diagramem.