Uživatelské nástroje
Obsah
Množiny, relace a zobrazení
Množina
- Matematická struktura ve které se prvky neopakují, soubor objektů
- Může být uspořádaná nebo neuspořádaná (vetšinou neuspořádaná)
- Počet prvků definuje její velikost v případě, že je konečná. Jestliže máme dvě množiny A, B a existuje vzájemné přirazení prvků množiny B prvkům množiny A, pak říkáme, že množiny A, B mají stejnou mohutnost. Množina stejné mohutnosti jakou má množina přirozených čísel se nazývá spočetná. Nekonečná množina, která není spočetná se nazývá nespočetná (příkladem nespočetné množiny je množina všech reálných čísel. Naproti tomu množiny celých čísel Z a racionálních čísel Q jsou obě spočetné.)
- Množinové operace (průnik, rozdíl, symetrický rozdíl (XOR), doplněk (nadmnožina bez podmnožiny) …)
- Potenční množina – množina všech podmnožin (včetně prázdné a sama sebe), potenční množina množiny o n prvcích má 2n prvků.
- Například celá čísla, reálná čísla, racionální čísla… to jsou všechno množiny.
- Lze ji definovat výčtem nebo omezením
- Uzavřenost množiny – když s prvky množiny provedu nějakou operaci, budou výsledkem zase prvky množiny.
Operace s množinami
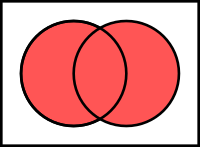
Sjednocení
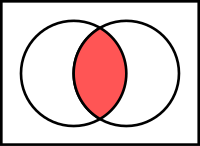
Průnik
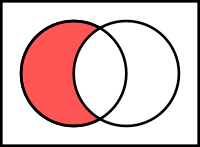
Rozdíl
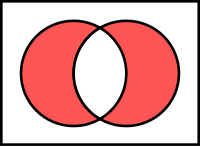
Symetrická diference množin
Vlastnosti operací
Komutativnost
X ∪ Y = Y ∪ X
X ∩ Y = Y ∩ X
Rozdíl komutativní není!
Asociativita
(X ∪ Y) ∪ Z = X ∪ (Y ∪ Z)
(X ∩ Y) ∩ Z = X ∩ (Y ∩ Z)
Distributivnost
(X ∪ Y) ∩ Z = (X ∩ Z) ∪ (Y ∩ Z)
(X ∩ Y) ∪ Z = (X ∪ Z) ∩ (Y ∪ Z)
De Morganovy zákony
<m>overline{X ∪ Y} = overline{X} ∩ overline{Y}</m>
<m>overline{X ∩ Y} = overline{X} ∪ overline{Y}</m>
Relace
- Binární – vztah mezi 2 prvky z množin
- Relace na množině – prvky množiny mají mezi sebou definované vztahy
- Symetrická – když mezi sebou prohodím prvky které jsou v relaci, budou stále v relaci (2 a 4 jsou sudá čísla, 4 a 2 jsou taky sudá čísla)
- Antisymetrická – když je prohodím v relaci nebudou (2 < 4, ale 4 < 2 neplatí, vyjímkou je, pokud jsou oba prvky stejné, pak jaksi ani to prohození není znát)
- Reflexivní – Jsou v relaci sami se sebou
- Tranzitivní – Když je A v relaci s B, a B v relaci s C, tak i A je v relaci s C
- Pokud je relace reflexivní, symetrická a tranzitivní, říká se jí relace ekvivalence.
Zobrazení
Zobrazení je přířazení prvků jedné množiny k prvkům z druhé. Funkce je speciálním případem zobrazení. Každé x má svoje y: každý prvek ze zobrazované množiny má přiřazený nějaký jeden prvek z druhé množiny (do které se zobrazuje). Rozlišují se tři základní typy:
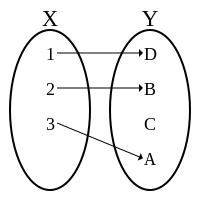
Injektivní (prosté)
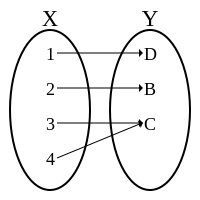
Surjektivní
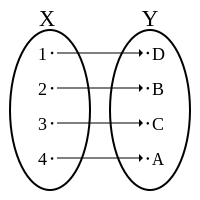
Bijektivní
Svaz
Svaz je laicky uspořádatelná množina. U státnic ale řekneme, že množina X s relací R je svazem, pokud pro každou dvouprvkovou podmnožinu (v relaci R) lze definovat maximum a minimum. Btw. když jsou dva prvky stejné, tak to pořád je svaz (maximum i minimum jsou oba prvky).
Pozn.: tohle nebylo přímo zadané, ale bylo to na přijímačkách, takže dobré vědět.
Grupa
Grupa je množina s binární operací a je na ni uzavřená.
Grupa splňuje tři axiomy:
- Asociativita: (a + b) + c = a + (b + c)
- Existence neutrálního prvku: a + 0 = a
- Existence inverzních prvků: a + (−a) = 0