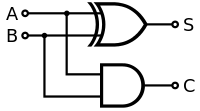Uživatelské nástroje
Obsah
Kombinační logické obvody
Jsou to takové logické obvody, která okamžitě reagují na vstup. Jinými slovy neberou potaz v historii, nemají paměť. Skladají se pouze z logických hradel (z čeho jiného taky) a neobsahují zpětnou vazbu. Jakoukoliv implementaci je možné vyjádřit pomocí hradel NAND a invertorů. To se dá odůvodnit přes tzv. duální tvrzení (viz booleovská logika 
| A | B | A or B | not(A) nand not(B) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
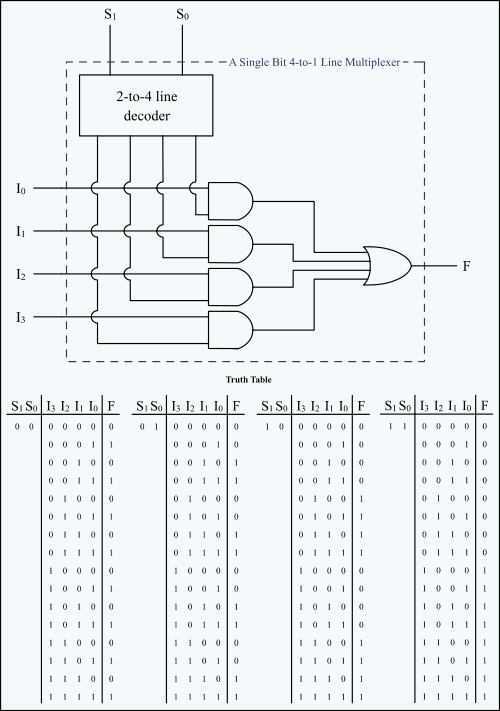
Multiplexor
Z několika vstupů vybírá jeden. Realizace pomocí dekodéru a AND hradel a OR hradla. S0 a S1 jsou bity „adresy“, podle které se vybírá jeden ze vstupů I0–3 a posílá se na výstup. Počet vstupů je 2n, kde n je počet bitů adresy. To protože je 2n kombinací hodnot bitů adresy.
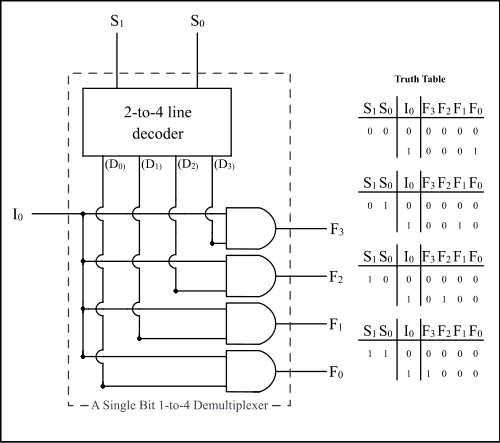
Demultiplexor
Jeden vstup přiřadí do správného výstupu. Dekodér a AND hradla. Opět zde figuruje adresa S0 – n, tentokrát její rozsah určuje počet výstupů. Princip je přesně opačný, než u multiplexoru.
Kodér (enkodér)
Slouží k zakódování zprávy. Jednoduchým kodérem se myslí takový, který očekává pouze na jednom ze vstupů log. 1 a podle toho, na kterém vstupu to bylo, nastaví hodnoty na výstupech. Z takového signálu lze pak původní zprávu dekódovat. Vstupů je 2n, kde n je počet výstupů.
Používá se také na obsluhu sedmi-segmentového displaye. Na vstup se mu přivede např binárně zakódovaná čislice, a na výstup vyleze napětí na těch drátech, které rozsvěcují patřičné segmenty.
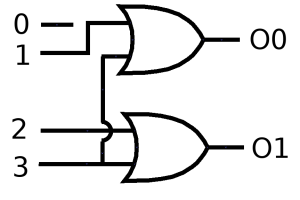
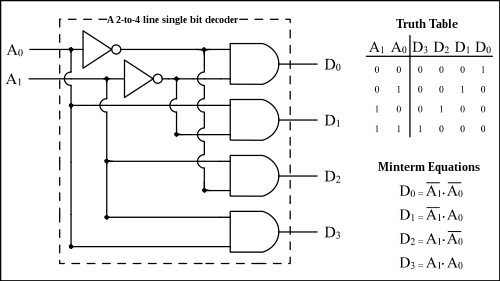
Dekodér
Slouží k rekonstrukci zakódované zprávy. Nejčastěji se používají binarní dekodéry n do 2n (např. 2 do 4, 3 do 8, …).
Binární sčítačka
Poloviční
Úplná
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Jde o dvě poloviční sčítačky za sebou a jeden OR. Dá se to jednodušše představit jako dva různé obvody – jeden pro součet a jeden pro carry.
Shrnutí (na co nezapomenout)
- kombinační obvody nemají zpětnou vazbu (a tedy ani paměť)
- reagují na vstup téměř okamžitě patřičnou úpravou výstupu (pouze fyziklní limity)
- skládají se z log. hradel, vše se dá udělat pomocí NANDů díky duálnímu tvrzení booleovy algebry: A or B = not(A) nand not(B), např AND se implementuje jako not(NAND), NAND lze použít i jako invertor, ale přímé použití invertoru je „levnější“
- kodér vs dekodér: kódování z jednoho do druhého a naopak. Například kód 1 z N na binární číslo (běžně má kodér 2n vstupů a n výstupů, dekodér naopak
- multiplexor vs demultiplexor: výběr jednoho signálu z mnoha vs poslání vstupu na jeden z výstupů, má adresní vodiče, vnitřně využívá dekodér (jak multiplexor, tak demultiplexor)
- sčítačka: jednobitová poloviční: XOR a AND, výstup z XORu je výsledek, z ANDu je carry
- úplná sčítačka: dvě poloviční za sebou, znát schéma! (výsledek je prostě součet těch 3 vstupů, tedy A, B a Cin, vyšší bit výsledku je Cout, nižší S)
Co je třeba vědět kdyby se zeptali
- duální tvrzení - výsledek operace se nezmění, pokud invertujeme vstupy, výstupy i operaci (or↔and, tedy A or B = not(A) nand not(B))
- vědět, jak se dělá pravdivostní tabulka, aby ji člověk uměl nakreslit např. pro poloviční sčítačku