Uživatelské nástroje
Obsah
Pseudokódy s využitím SIMLIB/C++
Reference
Náhodná čísla
double Random(); //pseudonáhodné číslo od 0 do 1 double Exponential(stredni); //exponenciální rozložení se střední hodnotou double Normal(stredni, rozptyl); //normální rozložení se střední hodnotou a rozptylem double Uniform(a, b); //rovnoměrné rozložení na intervalu <a, b)
Fronta (Queue)
Queue fronta; //vytvoření fronty (nekonečné?) fronta.Insert(this); //vložení aktuálního procesu do fronty fronta.Empty(); //true, když je fronta prázndá fronta.getFirst(); //vrátí položku (proces), která je ve frontě první Into(fronta); //vloží objekt (proces) do fronty
Zařízení (Facility)
Facility zarizeni("jmeno_zarizeni"); //vytvoření zařízení, jmeno_zarizeni se zobrazuje ve statistikách, zařízení si samo vytvoří vlastní frontu Facility zarizeni("jmeno_zarizeni", Queue *fronta); //vnucení jiné fronty Facility zarizeni[pocet_zarizeni]; //více zařízení, pak se jména a fronty nastavují takto: zarizeni[index].SetName("jmeno_zarizeni"); //nastavení jména zařízení zarizeni[index].SetQueue(fronta); //nastavení jiné fronty Seize(zarizeni, priorita); //obsazení zařízení s danou prioritou obsluhy (lze vynechat, pak 0), když je obsazeno, automaticky řadí do fronty Release(zarizeni); //uvolnění zařízení zarizeni.Busy(); //vrátí true, pokud je zařízení obsazeno, jinak false zarizeni.QueueLen(); //vrátí délku fronty čekající na zařízení
Sklad (Store)
Jako zařízení, ale pojme více transakcí.
Store sklad("jmeno_skladu", kapacita); //vytvořeni skladu, kapacitu lze vynechat (nekonečný sklad?), vytvoří si vlastní frontu Enter(sklad, polozek); //obsadí ve skladu místo (když je plno, automaticky zařadí do fronty) Leave(sklad, polozek); //uvolní ve skladu místo
Událost (Event)
class udalost: public Event { void Behavior() { //tělo události Activate(cas); //periodické opakování události Cancel(); //zružení události } };
Proces
class proces: public Process { //parametry procesu void Behavior() { //tělo procesu Passivate(); //uspí proces Activate(); //probudí proces Wait(doba); //čeká daný počet tiků Cancel(); //zružení procesu Priority = p; //nastavení priority zařízení, standardně 0 } };
Experiment
int main() { Init(start, end); //inicializace simulace //inicializace udalostí atd. Run(); //spuštění simulace objekt.Output() //tisk statistik front, zařízení, procesů a bůh ví čeho všeho ještě return 0; }
Příklady
Kalendář
while (kalendář je neprázdný a čas <= T_END) {
Vyjmi první záznam z kalendáře
Nastav čas na aktivační čas události
Proveď popis chování události
}
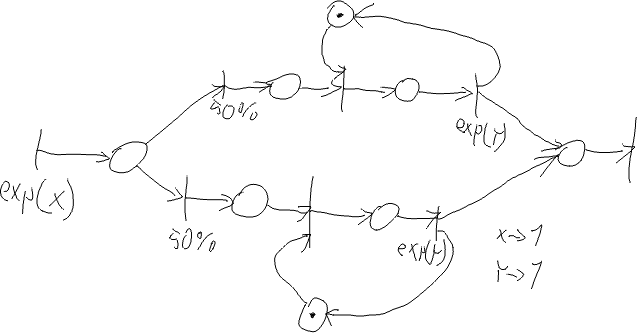
M/M/2 (každé zařízení má vlastní frontu)
Facility zarizeni[2]; class proces: public Process { void Behavior() { int kam = (int) Random() * 2; Seize(zarizeni[kam]); Wait(Exponential(y)); Release(zarizeni[kam]); } };
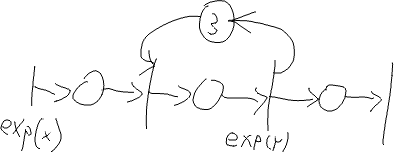
M/M/3 se společnou frontou a statistikami pro každé zařízení zvlášť
Facility F[3]; Queue Q; class Proc: public Process { void Behavior() { int id = 0; for (int i = 0; i < 3; i++) { //pokus o nalezeni volneho zarizeni if (!F[i].isBusy()) { id = i; } } Seize(F[id]); //pri Seize() obsazeneho zarizeni se pozadavek automaticky radi do fronty, takze to nemusime resit Wait(Exponential(y)); Release(F[id]); } }; class Gen: public Event { void Behavior() { (new Proc) -> Activate(); Activate(Time + Exponential(x)); } }; void main(void) { for (int i = 0; i < 3; i++) { F[i].setQueue(Q); } Init(0, 100); (new Gen) -> Activate(); Run(); Q.Output(); for (int i = 0; i < 3; i++) { F[i].Output(); } return 0; }
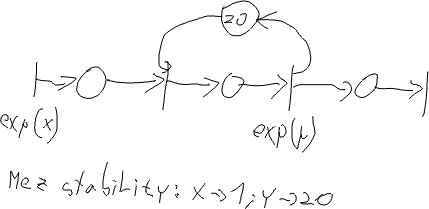
M/M/20 s jednou společnou frontou, na mezi stability
Store sklad('Sklad', 20); class obsluha: public Process { void Behavior() { Enter(sklad, 1); Wait(Exponential(20)); Leave(sklad, 1); } }; class prichody: public Event { void Behavior() { (new obsluha) -> Activate(); Activate(Time + Exponential(1)); } }; int main() { Init(0, 1000); (new prichody) -> Activate(); Run(); sklad.Output(); return 0; }
Spojitá simulace s Eulerovou metodou v jednom procesu
Předpokládejme, že máme k dispozici diskrétní simulační systém umožňující pouze popis systému pomocí procesů (inspirujte se částí SIMLIB/C++).
Naprogramujte v rámci jednoho procesu spojitou simulaci s využitím Eulerovy metody. Máte k dispozici 2 globální pole pro n integrátorů:
double vstup[N];double vystup[N];
a funkci dynamic(), která vypočtš vstupy integrátorů. Nezapomeňte na inicializaci, dokročení na koncový čas Tend (bez dokročení 0b) a tisk výsledků PrintResults().
#define N 10 class Euler: public Process { double vstup[N]; double vystup[N]; double krok = 0.01; Euler() { //konstruktor for (int i = 0; i < N; i++) { //inicializace pole s vystupy (NUTNOST – protoze dal se pouziva vystup[] += …) vystup[i] = 0; } } Behavior() { //samotny proces while (Time < Tend) { Dynamic(); if (Time + krok > Tend) { //pokud se jedna o dokroceni, uprav velikost kroku krok = Tend - Time; } for (int i = 0; i < N; i++) { //spocita nove vystupy vystup[i] += krok * vstup[i]; } PrintResults(); //vytiskne je Wait(krok); //a az ted posune cas (Time je v procesu read-only, takze ho nemuze posunout!) } } }
Kalendář událostí se spojitou simulací
Za predpokladu, ze znate princip algoritmu rizeni diskretni simulace (next-event) s kalendarem udalosti a princip vypoctu spojite simulace, napiste pseudokod algoritmu rizeni kombinovane simulace bez uvazovani stavovych podminek. Pro zjednoduseni mate k dispozici funkce:
Vypocet_vstupu_integratoru()Krok_eulerovy_metody(delka_kroku)(ktera funguje i pri nulove delce kroku a neposouva cas)
Take muzete predpokladat, ze simulace bude ukoncena specialni naplanovanou udalosti. Nezapomente nastavovat cas a dokrocit na cas udalosti!
Inicializace_casu_a_kalendare; while (1) { Vyber_event_z_kalendare; krok = normalni_delka_kroku; while (cas < cas_eventu) { if (cas + krok > cas_eventu) { krok = cas_eventu - cas; } Vypocet_vstupu_integratoru(); Krok_eulerovy_metody(krok); cas += krok; } if (event == specialni_udalost) { break; } else { Vykonej_event; } }
Algoritmus řízení spojité simulace s Eulerem
inicializace poc. stavu a promennych a casu; while (cas < koncovy_cas) { Print_results(); Update_integrators(); if ((cas + krok) > koncovy_cas) { krok = koncovy_cas - cas; } euler(); cas += krok; }
Stavové podmínky
Slajdy, str. 263
Inicializace stavu a podmínek while (čas < koncový_čas) { //Uložení stavu a času *** Krok numerické integrace /* !!! Sem příjde vložit Euler, Runge-Kutta, nebo jiná metoda !!! */ //Vyhodnocení podmínek === if (podmínka změněna) { if (krok <= minimální_krok) { //Potvrzení změn podmínek === //Stavová událost +++ krok = běžná_velikost_kroku } else { //Obnova stavu a času *** krok /= 2 if (krok < minimální_krok) { krok = minimální_krok } } } }
Nevíte někdo co chce říct těma hvězdičkama, plusama a rovnítkama?
NAND
class Nand: public Process { public: Nand(): Process() { OUT = VAL_X; IN[0] = IN[1] = VAL_X; } void Behavior(){ while (1) { Passivate(); if(IN[0] == VAL_X || IN[1] == VAL_X) { OUT = VAL_X; } else { OUT = !(IN[0] && IN[1]); } Print("Time==%f.out=%dn", Time, OUT); } } void input(intidx, int val) { IN[idx] = val; Activate(Time + DELAY); } int OUT; int IN[2]; }; class Value: public Event{ public: Value(Nand *n, int idx, int val): N(n), Event(), Idx(idx), Val(val) {} void Behavior() { N -> inout(Idx, Val); Cancel(); } Nand *N; int Idx, Val; }; int main() { Init(0, 1); Nand *n = new Nand; n -> Activate(); (new Value(n, 0, 0) -> Activate(0, 1); (new Value(n, 1, 1) -> Activate(0, 2); (new Value(n, 0, 1) -> Activate(0, 3); Run(); }
Funkcionální model
Závaží na pružině
//popis modelu v SIMLIB/C++ struct Model { Integrator y, v; Model(double m, double K, double y0): v(-g - K/m * y, 0), y(v, y0) {} }; Model s(1, 1e3, -1); //instance modelu s parametry
Monte Carlo
Objem 3D tělěsa
Metodou Monte Carlo vypočtěte objem složitého tělesa v 3D prostoru za předpokladu, že znáte funkci bool BodJeUvnitrTelesa(double x, double y, double z) a rozsah mezí integrálu ve všech 3 osách je uložen v polích double min[3] a double max[3]. Funkci pro výpočet integrálu napište v ISO C: double integMC(long POCET_EXPERIMENTU, double xmin[3], double xmax[3]);. Nesmíte použít žádnou funkci kromě double Random() vracející pseudonáhodné číslo v rozsahu 0…1. Rozsah kódu je maximálně 15 řádků.
double integMC(long POCET_EXPERIMENTU, double xmin[3], double xmax[3]) { int jeUvnitr = 0; double x, y, z; for (int i = 0; i < POCET_EXPERIMENTU; i++) { x = xmin[0] + (xmax[0] - xmin[0]) * Random(); y = xmin[1] + (xmax[1] - xmin[1]) * Random(); z = xmin[2] + (xmax[2] - xmin[2]) * Random(); if (BodJeUvnitrTelesa(x, y, z)) { jeUvnitr++; } } double P = jeUvnitr / POCET_EXPERIMENTU; double rozsah = (xmax[0] - xmin[0]) * (xmax[1] - xmin[1]) * (xmax[2] - xmin[2]); return P * rozsah; }
Integrál
Napište pseudokód pro výpočet 5násobného určitého integrálu funkce f(x1, x2, …, x5) (podle všech xi, i je z {1, …, 5}) metodou Monte Carlo (integrál musí být 5násobný, jinak 0 b). Doplňte meze integrálu. Předpokládejte, že neznáte rozsah funkčních hodnot funkce f(). Máte k dispozici pouze funkci float Radnom() vracející pseudonáhodné číslo v rozsahu 0…1 a žádnou jinou. Kolik pokusů musíte udělat, aby relativní chyba výpočtu nepřekročila 0,001?
long double MCInteg(double (*f)(double[]), double xmin[], double xmax[]) { long double sum = 0, meze = 1; const int n = 5; double x[n]; long poc_pokusu = 1000000; //chyba = 1 / sqrt(pokusu) for (long i = 0; i < poc_pokusu; i++) { for (long j = 0; j < n; j++) { x[j] = Random() * (xmax[j] - xmin[j]) + xmin[j]; } sum += f(x); } for (unsigned int i = 0; i < n; i++) { meze *= xmax[i] - xmin[i]; } return sum / poc_pokusu * meze; }