Úkol 2

Bc. Jan Kaláb <[email protected]>

Uvažte jazyk L₁ = {wcⁱ | w ∈ {a, b}* ∧ (#_a(w) = i ∨ #_b(w) = i)}.

Sestavte gramatiku G₁ takovou, že L(G₁) = L₁.

G₁ = ({S, A, B}, {a, b, c}, P, S)

P:

• S → A | B | ε
• A → aAc | bA | ε
• B → bBc | aB | ε

Algoritmickým postupem převeďte gramatiku G₁ na zásobníkový automat provádějící syntaktickou analýzu zdola nahoru.

M = ({q, r}, {a, b, c}, {S, A, B, a, b, c, #}, δ, q, #, {r})

Reduce:

• δ(q, ε, A) = {(q, S)}
• δ(q, ε, B) = {(q, S)}
• δ(q, ε, bA) = {(q, A)}
• δ(q, ε, aAc) = {(q, A)}
• δ(q, ε, aB) = {(q, B)}
• δ(q, ε, bBc) = {(q, B)}
• δ(q, ε, ε) = {(q, A), (q, B), (q, S)}

Shift:

• δ(q, a, ε) = {(q, a)}
• δ(q, b, ε) = {(q, b)}
• δ(q, c, ε) = {(q, c)}

Accept:

• δ(q, ε, S#) = {(r, ε)}

Lze jazyk L₁ přijmout deterministickým zásobníkovým automatem (DZA)? Zdůvodněte své tvrzení (formální důkaz se nepožaduje).

Nelze. Kvůli ∨ v zadání nevíme, zda použít podmínku #_a(w) nebo #_b(w), a nevíme tedy, zda na zasobníku počítat b nebo a.

Mějme jazyky L₁ = {aⁱbʲcⁱdʲ | i, j ∈ ℕ} a L₂ = {aⁱbⁱcʲdʲ | i, j ∈ ℕ}.¹⁾ Pro každý z jazyků L₁ a L₂ dokažte, nebo vyvraťte, zda je bezkontextový.

Důkaz sporem.

Předpokládejme, že jazyk L₁ je bezkontextový. Pak podle pumping lemmatu pro bezkontextové jazyky existuje konstanta k taková, že je-li z ∈ L₁ a |z| ≥ k, pak lze z napsat ve tvaru: z = uvwxy, vx ≠ ε, |vwx| ≤ k a pro všechna i ≥ 0 je uvⁱwxⁱy ∈ L₁.

Zvolíme si z = uᵏvᵏwᵏxᵏyᵏ, |z| > k, i > 1, pak může dojít k následujícímu rozdělení:

• vwx = aᵐ, m ≤ k, #_a(z) ≠ #_c(z)
• vwx = aᵐbⁿ, m + n ≤ k, #_a(z) ≠ #_c(z) ∨ #_b(z) ≠ #_d(z)
• vwx = bᵐ, m ≤ k, #_b(z) ≠ #_d(z)
• vwx = bᵐcⁿ, m + n ≤ k, #_a(z) ≠ #_c(z) ∨ #_b(z) ≠ #_d(z)
• vwx = cᵐ, m ≤ k, #_a(z) ≠ #_c(z)
• vwx = cᵐdⁿ, m + n ≤ k, #_a(z) ≠ #_c(z) ∨ #_b(z) ≠ #_d(z)
• vwx = dᵐ, m ≤ k, #_b(z) ≠ #_d(z)

Ukázali jsme, že nelze najít takové rozdělení, které by splňovalo podmínky pumping lemmatu pro bezkontextový jazyk, což je spor, a jazyk tedy není bezkontextový.

G = ({A, S, T}, {a, b, c, d}, P, A)

• A → ST
• S → aSb | ε
• T → cTd | ε

K jazyku L₂ lze sestavit bezkontextovou gramatiku, tudíž je bezkontextový.

Mějme jazyky L₃ ∈ ℒ₃ a L₂ ∈ ℒ₂. Dokažte, že problém L₂ ⊆^? L₃ je (eventuelně není) rozhodnutelný? K důkazu použijte uzávěrové vlastnosti bezkontextový a regulárních jazyků.

• Platí definice podmnožiny: L₂ ⊆ L₃ ⇔ L₂ ∩ L₃′ = ∅²⁾
• ℒ₃ jsou na doplněk uzavřené
• ℒ₂ jsou uzavřené na průnik s ℒ₃
• Problém se tedy redukoval na prázdnost ℒ₂, a ten je rozhodnutelný.
• Problém L₂ ⊆^? L₃ je tady také rozhodnutelný.

Uvažujte jazyk L₄, který je generován gramatikou
G₄ = ({E, T, F}, {(, ), true, or, and, not}, P, E), kde

P:

• E → E or T | T
• T → T and F | F
• F → (E) | not(E) | true

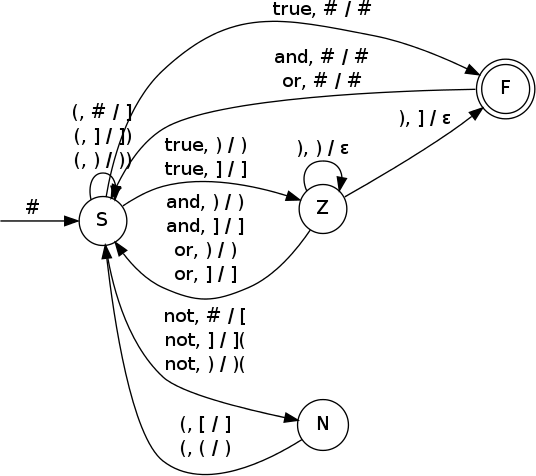
Sestrojte deterministický zásobníkový automat přijímající jazyk L₄ a demonstrujte jeho funkci na přijetí řetězce (true or not(true)) and true.

³⁾

1. δ(S, (, #)
2. δ(S, true, ])
3. δ(Z, or, ])
4. δ(S, not, ])
5. δ(N, (, ()
6. δ(S, true, ))
7. δ(Z, ), ))
8. δ(Z, ), ])
9. δ(F, and, #)
10. δ(S, true, #)

Mějme gramatiku G₅ = ({S, A, B, C}, {a, b, c}, P, S), kde

P:

• S → aACa
• A → B | a
• B → C | c
• C → Cc | bC | ε

Převeďte gramatiku G₅ algoritmicky do Chomského normální formy.

Bez ε přechodů:

• N_ε⁰ = ∅
• N_ε¹ = {C}
• N_ε² = {C, B}
• N_ε³ = {C, B, A}
• N_ε⁴ = {C, B, A} = N_ε³ = N_ε

• S → aACa | aAa | aCa | aa
• A → B | a
• B → C | c
• C → Cc | b | bC | c

Bez jednoduchých pravidel:

• N_S⁰ = {S}
• N_S¹ = {S} = N_S⁰ = N_S

• N_A⁰ = {A}
• N_A¹ = {A, B}
• N_A² = {A, B, C}
• N_A³ = {A, B, C} = N_A² = N_A

• N_B⁰ = {B}
• N_B¹ = {B, C}
• N_B² = {B, C} = N_B¹ = N_B

• N_C⁰ = {C}
• N_C¹ = {C} = N_C⁰ = N_C

• S → aACa | aAa | aCa | aa
• A → Cc | a | b | bC | c
• B → Cc | b | bC | c
• C → Cc | b | bC | c

Vlastní gramatika (odstranění zbytečných a nedostupných symbolů):

• V₀ = {S}
• V₁ = {S, a, A, C}
• V₂ = {S, a, A, C, c, b}
• V₃ = {S, a, A, C, c, b} = V₂ = V

• S → aACa | aAa | aCa | aa
• A → Cc | a | b | bC | c
• C → Cc | b | bC | c

Chomského normální forma:

G = ({S, <ACa>, <Aa>, <Ca>, A, C, a′, b′, c′}, {a, b, c}, P, S)

P:

• S → a′<ACa> | a′<Aa> | a′<Ca> | a′a′
• <ACa> → A<Ca>
• <Aa> → Aa′
• <Ca> → Ca′
• A → Cc' | a | b | b′C | c
• C → Cc' | b | b′C | c
• a′ → a
• b′ → b
• c′ → c

Převeďte gramatiku G₅ algoritmicky do Greibachové normální formy.

Vlastní gramatika:

• Viz převod do Chomského normální formy

Odstranění levé rekurze (S < A < C):

• S → aACa | aAa | aCa | aa
• A → Cc | a | b | bC | c
• C → b | bC | bC′ | bCC′ | c | cC′
• C′ → c | cC′

Greibachové normální forma:

G = ({S, A, C, C′, a′, c′}, {a, b, c}, P, S)

P:

• S → aACa′ | aAa′ | aCa′ | aa′
• A → a | b | bC | bC′c′ | bCC′c′ | bCc′ | bc′ | c | cC′c′ | cc′
• C → b | bC | bC′ | bCC′ | c | cC′
• C′ → c | cC′
• a′ → a
• c′ → c