Obsah
Transformace obrazu
Podle lokality:
- Bodové – výstupní hodnota na určitých souřadnicích je závislá jen na vstupní hodnotě o stejných souřadnicích
- Lokální – výstupní hodnota na určitých souřadnicích je závislá na vstupních hodnotách okolí bodu o stejných souřadnicích
- Globální – výstupní hodnota na určitých souřadnicích je závislá na všech hodnotách vstupního obrazu
Podle typu:
- Barevné
- Geometrické
- Frekvenční (DFT, DCT, Gabor)
- Integrální (vlnková)
Důvody transformace: korekce obrazu, extrakce informací, …
Bodové transformace
Jasové operace
- Slouží například pro zvýšení kontrastu, negativ
- Intenzita (jas) odpovídá odstínu šedé barvy I = 0,299R + 0,587G + 0,114B
Prahování
- Vstupem při prahování může být barevný obraz či obraz s odstíny šedé
- Výsledkem je většinou binární obraz reprezentující hodnoty nad/pod zvoleným prahem
Nelineární transformace
- Logaritmická – Slouží pro zvyšování detailů v tmavých oblastech obrázku a snížení detailů ve světlých oblastech
- Exponenciální – Zvyšování detailů ve světlých oblastech, snížení detailů v tmavých oblastech
Lokální operace
- Nová hodnota bodu se odhaduje z malého okolí (okno např. 3 × 3 body), problémy na okrajích obrazu – přesah masky.
- Příspěvek jednotlivých bodů v okolí je vážen v lineární kombinaci koeficienty matice h – nazývané jako maska či konvoluční jádro.
2D Konvoluce
Convolution, Convolution matrix
| Rozostření | ||
|---|---|---|
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| Doostření | ||
|---|---|---|
| 0 | −1 | 0 |
| −1 | 5 | −1 |
| 0 | −1 | 0 |
Výsledek se pak ještě musí normalizovat (podělit sumou matice)!
Globální operace
- Globální operace využívají informaci z celého obrazu, výsledná informace pak slouží ke změně hodnot jednotlivých bodů v obraze.
- Slouží pro např. ekvalizaci histogramu, zvýraznění kontrastu, …
Ekvalizace histogramu
Histogram
- Jedná se o statistickou reprezentaci obrazu, která představuje graf četnosti výskytu jednotlivých barev (odstínů, intenzit …)
- Histogram je grafické znázornění vektoru s počtem složek rovným počtu možných úrovní intenzit obrazových bodů a slouží k hodnocení rozložení intenzit v digitálním obraze (posuzování kvality obrazu).
Ekvalizace histogramu
- Algoritmus, který změní rozložení intenzit v obraze tak, aby se v něm vyskytovaly pokud možno intenzity v širokém rozmezí, a to přibližně se stejnou četností.
- Cílem je zvýšit kontrast úplným využitím jasové stupnice, jasově obraz normalizovat (například pro automatické srovnání)
Geometrické transformace
Geometrické operace mapují bod v obraze o souřadnicích (x, y) do výstupního obrazu na novou pozici (x′, y′)
Homogenní souřadnice
- Bežně se používají v projektivní geometrii, počítačové grafice, robotice aj.
- Základní myšlenkou je reprezentovat bod ve vektorovém prostoru o jednu dimenzi větším.
- Bod [x, y]ᵀ se v homogenních souřadnicích vyjádří ve 3D vektorovém prostoru jako [λx, λy, λz]ᵀ, kde λ ≠ 0.
- Pro jednoduchost se používá jedno z nekonečně mnoha vyjádření [x, y, 1]ᵀ
- Homogenní souřadnice bodu ve 3D s kartézskými souřadnicemi [x, y, z] je uspořádaná čtveřice [X, Y, Z, w] pro kterou platí x = X/w, y = Y/w, z = Z/w.
Afinní transformace
Čáry, které jsou rovné a paralelní zůstanou rovné a paralelní i po transformaci, ovšem nemusí být rovnoběžné s původními.
Příklady:
| Identita | ||
|---|---|---|
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| Posun | ||
|---|---|---|
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| xᵀ | yᵀ | 1 |
| Velikost | ||
|---|---|---|
| Sx | 0 | 0 |
| 1 | Sy | 0 |
| 0 | 0 | 1 |
| Rotace | ||
|---|---|---|
| cos(Θ) | sin(Θ) | 0 |
| −sin(Θ) | cos(Θ) | 0 |
| 0 | 0 | 1 |
| Zkosení | ||
|---|---|---|
| 1 | Zx | 0 |
| Zy | 1 | 0 |
| 0 | 0 | 1 |
Skládání transformací
- Výsledná transformace vznikne skládáním násobením matic
- Záleží na pořadí – součin transformačních matic není komutativní
- „V OpenGL platí, že transformace jsou na vertexy aplikovány v opačném pořadí, než jsou zavolány jejich korespondující příkazy. Jestliže například bude v programovém kódu sekvence příkazů
glTranslatef(); glRotatef();, ve skutečnosti bude objekt (resp. jeho vertexy) nejprve otočen a teprve poté posunut.“1)
Frekvenční transformace
Diskrétní Fourierova transformace
Discrete Fourier transform
Popisuje signál ve frekvenční oblasti, výsledek se nazývá spektrum
<m>X(k) = \sum{n=0}{N-1}{x[n] e^{-j2\pi{nk}/{N}}}</m>
N je počet vzorků signálu, k ∈ <0, N−1>
- Srovnávání signálu s různě roztaženými komplexními exponenciálami
- Pro analýzu obrazu se používá 2D DFT (série 1D)
Diskrétní kosinová transformace
- Při DFT reálného signálu vznikají komplexní koeficienty, transformace je v tomto případě redundantní (kvůli symetrii s k = 0), u DCT koeficienty redundantní nejsou (vhodnější pro kompresní účely)
- Srovnávání signálu s různě roztaženými kosinusoidami
- Výsledek je také nazýván spektrem, ovšem nikoliv symetrické (jako u DFT)
- Pro analýzu obrazu se používá 2D DCT (série 1D)
Gaborova transformace
- Využívána k extrakci příznaků (následná klasifikace, segmentace či detekce hran)
- 2D Gaborova transformace udává, kolik energie nese obraz okolo daného místa na dané frekvenci v daném směru
- Speciální případ krátkodobé FT
- Gaborova transformace vzniká posouváním Gaussova okna při pevně zvoleném roztažení komplexní exponenciály
Integrální transformace
Vlnková transformace
- Wavelet Transform umožňuje získat časově-frekvenční popis signálu. Její přirozenou aplikací je zjištění polohy a délky trvání daného jevu.
- Uplatnění: extrakce příznaků, odstranění šumu nebo kompresi signálů
- Může být spojitá, diskrétní, stacionární
Homografie
- Projektivita, kolineace, projektivní transformace
- Vyjádření tramsformace mezi obrazy
- Mapuje body z jednoho obrazu do druhého, vyjadřuje lineární transformaci H mezi obrazy.
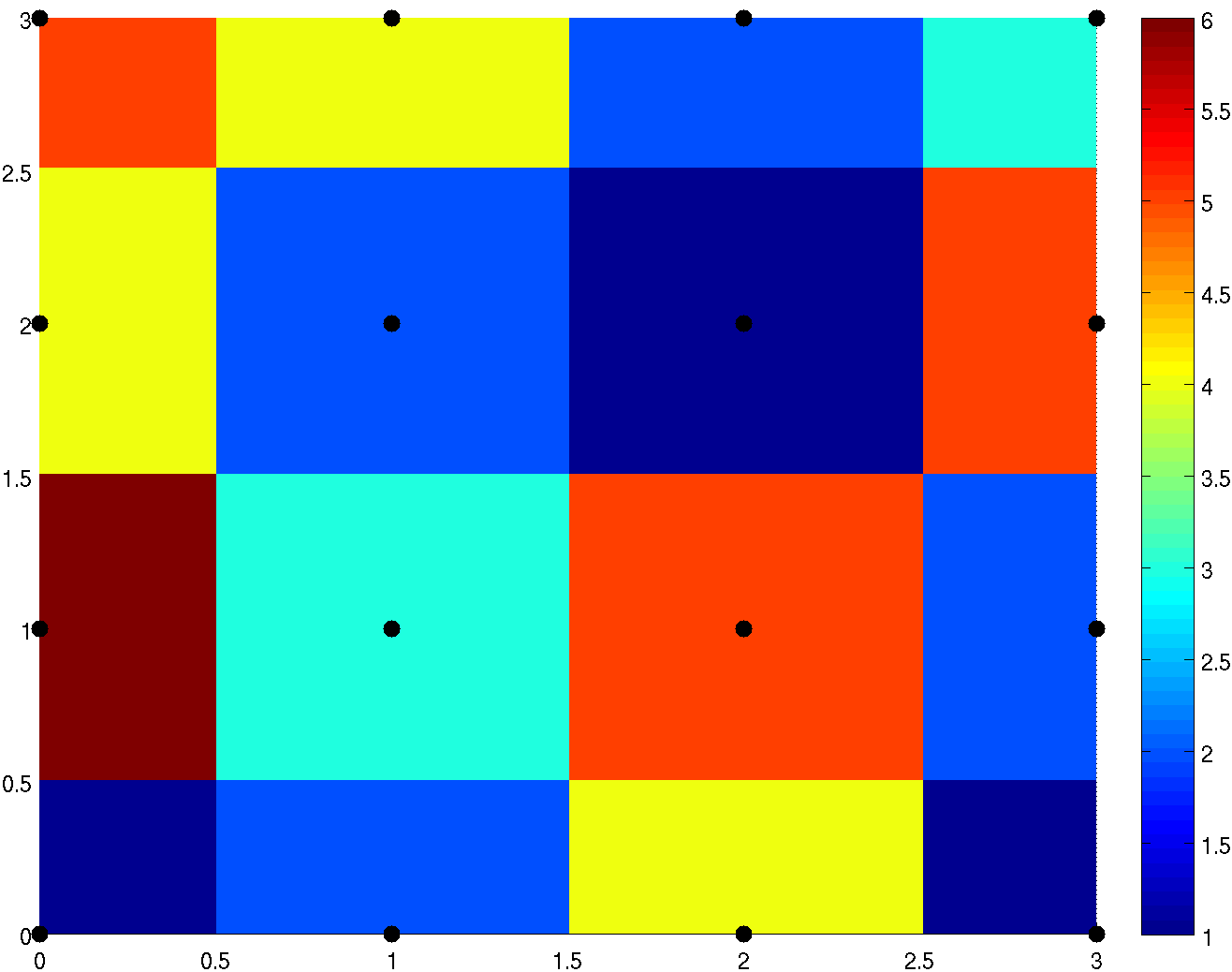
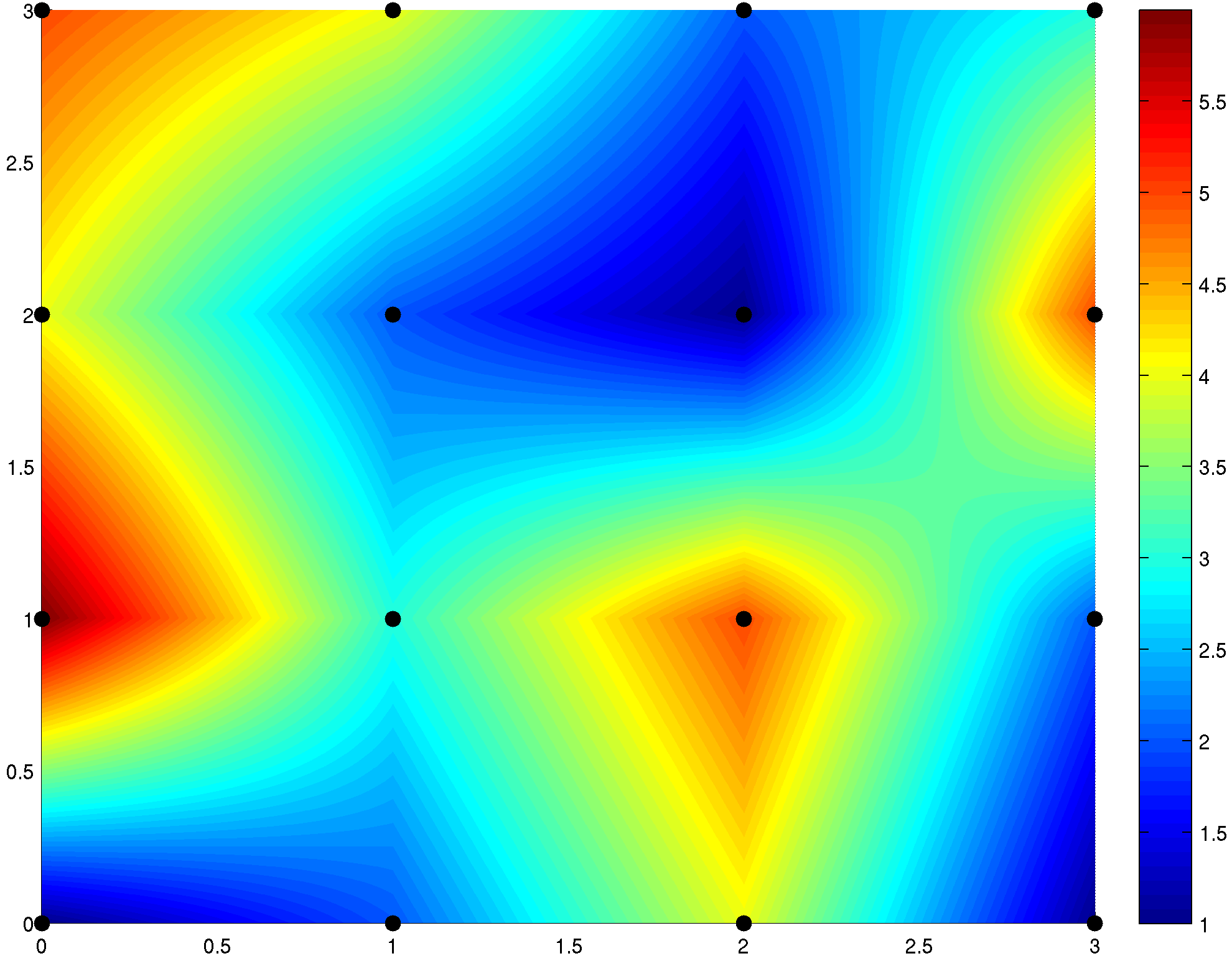
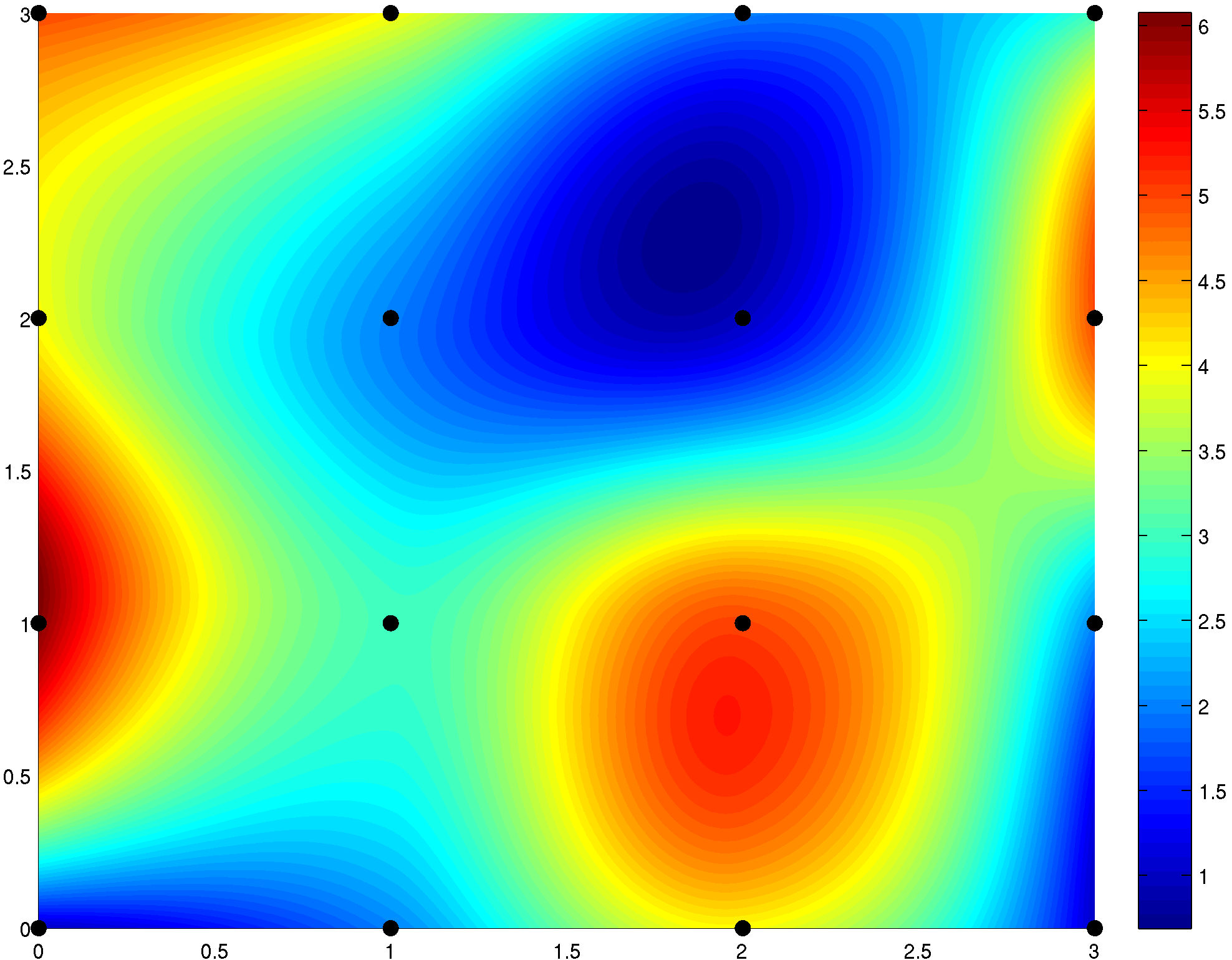
Interpolační metody
Použití pro získání hodnoty obrazové funkce mimo naměřené diskrétní hodnoty. V případě barevného obrazu se provádí interpolace pro všechny barevné složky zvlášť.