Obsah
Vyhledávání a řazení
Vyhledávání
Nejdůležitějším parametrem je přístupová doba, tedy doba potřebná k nalezení požadované informace. Přesněji je možné uvádět: „[Minimální|Maximální|Průměrná] doba (ne)úspěšného vyhledání.“
Sekvenční vyhledávání v poli
Po jednom prvku procházíme pole1) a kontrolujeme jestli se aktuální prvek shoduje s hledaným. Pokud je index prvku roven délce pole a ani tak jsme nenašli, je vyhledání neúspěšné.
- Minimální čas úspěšného vyhledání = 1 (hledaný byl hned první prvek)
- Maximální čas úspěšného vyhledání = N2) (hledný prvek byl až na posledním místě)
- Průměrný čas úspěšného vyhledání = N/2
- Čas neúspěšného vyhledání = N
Algoritmus je možné vylepšit tzv. zarážkou, která se přidá na konec pole. Pak samozřejmě vždy najdeme požadovaný prvek, a úspěch se pozná podle indexu prvku.
Dobrým vylepšením je v případě nalezení prvku tento prvek prohodit s jeho sousedem. Takto se často hledané prvky dostanou na začátek pole a budou tak nalézány dříve.
Pokud pole seřadíme, můžeme dříve detekovat nenalezení prvku.
Binární vyhledávání
Pracuje nad seřazeným polem a funguje na principu půlení intervalu.
{Nastavení zarážek} min := 1; {Pascal indexuje pole od 1} max := N; {N je velikost pole A} repeat mid := (min + max) div 2; {Najdi prostřední prvek} if x > A[mid] then {Pokud je hledaný prvek větší než prostřední} min := mid + 1 {Zpracujeme dále část pole která je větší než prostřední} else max := mid - 1; {V opačném případě zpracujeme část menší než prostřední} until (A[mid] = x) or (min > max); {Tohle opakujeme dokud prostřední prvek není tím hledaným nebo dokud není jak rozsah zmenšovat}
Tato metoda má logaritmickou složitost.
Binární vyhledávací strom
Je to stromová datová struktura, kde každý uzel má nejvíce 2 potomky3) a přitom levý potomek je menší a pravý je větší než rodičovský.
Vše potřebné je na výše uvedené Wikipedii.
Hashovací tabulky
Mapovací funkce
Je to funkce, která se provede nad daty která chceme do tabulky přidat, nebo vyhledat, a podle ní se rozhodne ke kterému řádku tabulky přistoupíme.
Funkce musí být:
- Rychlá
- Způsobovat co nejméně kolizí (jinými slovy, musí vytvářet co možná nejunikátnější hashe)
Prohledávání textu
Knuth-Morris-Pratt
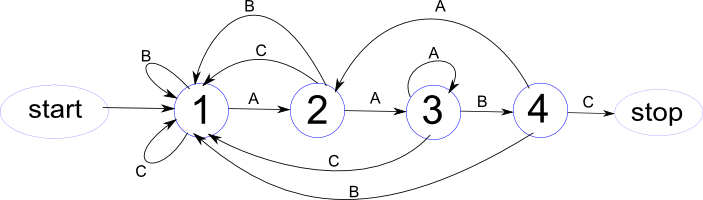
Ke své práci využívá konečný automat. Následující ukázka demonstruje automat pro hledaný vzorek AABC při použití abecedy {A,B,C}.
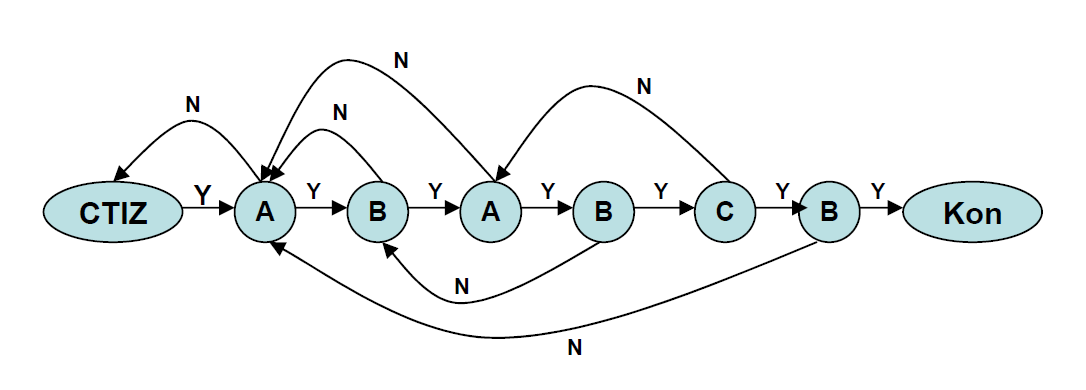
Nevýhodou takového řešení je skutečnost, že z každého uzlu vychází tolik hran, kolik je znaků abecedy. Lze vyjádřit i pomocí dvou hran - ANO(souhlas, Y), NE (nesouhlas, N). Vzorek ABABCB pro libolovolnou abeceny obsahující alespoň znaky A a B.
Boyer-Moor
Boyer–Moore string search algorithm
Viz opora IAL strana 174
Řazení
Shrnutí
- vyhledávání: sekvenční v poli, v binárním vyhledávacím stromu, přes hash funkci a tabulku (tabulka rozptýlených hodnot)
- prohledávání textu: naivní metoda, knuth-morris-pratt (konečný automat), boyer-moore (2 tabulky, porovnává se hledané slovo odzadu)
- řazení: bubble, insertion, select, merge, heap, quick
- Znát složitosti algoritmů